B31.3 Code Issue – Non-conservative Sustained Stress

I would like to highlight an issue in ASME B31.3 that’s been sitting there underneath most of our noses for several years. Depending on your interpretation of the Code (or that of your pipe stress software) this can result in significant under-prediction of sustained and occasional bending and torsional stresses at reducing intersections. [Edit March 2017: this article is based on B31.3 2014 and earlier. It still applies generally for B31.3 2016, however a new article will be published shortly to address changes]

branch

Background

The sustained bending stress for any element is calculated in equation 23b as

$\displaystyle S_b = \frac{\sqrt{(I_iM_i)^2+(I_oM_o)^2}}{Z}$

$I_i$ is the sustained in-plane moment index. In the absence of more applicable data, $I_i$ is taken as the greater of $0.75i_i$ or 1.00
$I_o$ is the sustained out-plane moment index. In the absence of more applicable data, $I_o$ is taken as the greater of $0.75i_o$ or 1.00.
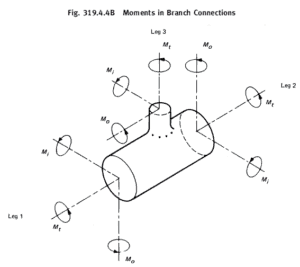
$i_i / i_o$ are the in-plane / out-plane stress intensification factors for the intersection
$Z$ = sustained section modulus. $Z$ in eqs. (23b) and (23c) is described in para. 319.4.4 but is computed in this paragraph using nominal pipe dimensions less allowances

The Code wording is quite vague here, as para 319.4.4 is written for displacement stresses and contains both formulae including the section modulus $Z$ as well as the use of an effective section modulus $Z_e$ for reducing branches.

For (the branch end of) reducing branches the displacement bending stress in para 319.4.4 is calculated as

$\displaystyle S_b = \frac{\sqrt{(i_iM_i)^2+(i_oM_o)^2}}{Z_e}$

$Z_e$ = effective section modulus of branch = $\pi r_2^2T_s$

$r_2$ = mean branch cross-sectional radius

$T_s$ = effective branch wall thickness, lesser of $T_h$ and $i_iT_b$

Another way to express this is as follows, assuming the moment is all in-plane for now:

$\displaystyle S_b=\frac{M_i}{\pi r_2^2T_b}$ , for $i_i\frac{T_b}{T_h} < 1$ $\displaystyle S_b=\frac{i_iM_i}{\pi r_2^2T_h}$ , for $i_i\frac{T_b}{T_h} >1$

Now applying this approach for sustained or occasional stresses, the question arises for reducing branches as to whether the plain section modulus should be used or the effective section modulus ? Certainly the Code formula only uses the symbol $Z$ in equations 23b and 23c, however this would result in a fairly conservative calculation. If instead an effective section modulus $Z_e$ is used, the next question is how should this be calculated. Taking the Code definition and directly applying it (as at least one major pipe stress program does) results in a non-conservative outcome for the case where $i_iT_b$ is less than $T_h$ (the left hand equation above).

Starting again from equation 23b and assuming all in-plane sustained bending moments on a reducing branch:

$\displaystyle S_b = \frac{I_iM_i}{Z}$

Taking $I_i = 0.75i_i$ , and utilising the effective modulus $Z_e = \pi r_2^2i_iT_b$ :

$\displaystyle S_b=\frac{0.75i_iM_i}{\pi r_2^2i_iT_b} = \frac{0.75M_i}{\pi r_2^2T_b}$

This is clearly only 75% of what the sustained stress should be for the branch pipe. In fact, the simplified thin wall approximation used for $Z_e$ further underestimates the stress and may reduce it by another 5% or so.

If the moment is all out-plane:

$\displaystyle S_b=\frac{0.75i_oM_o}{\pi r_2^2i_iT_b} = \frac{i_o}{i_i}\frac{0.75M_o}{\pi r_2^2T_b}$

Most intersections in B31.3 Appendix D have $i_i=0.75i_o+0.25$ , meaning $i_i$ is less than or equal to $i_o$ , which tends to improve matters somewhat for the out-plane calculation. Weldolets have the same SIF for in-plane and out-plane however.

Example

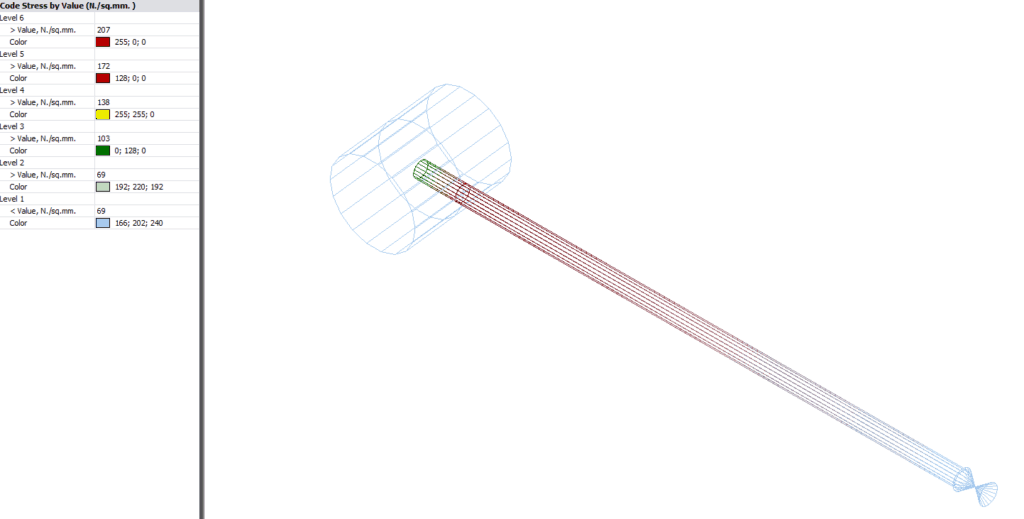
Intersection: DN300 x 50 Sch 40 weldolet (no corrosion).

In the image below from CAESAR II, the sustained stress is clearly lower (green) at the centreline intersection point than at the shell. This higher stress could easily have been missed if the additional node had not been modelled at the header shell location.

Reducing branch

Code Interpretation

For the B31.3 sustained stress calculation, I believe that the Code should be interpreted either as not requiring the use of the effective modulus for sustained stress calculations, or that the stress index $I_i$ should be used rather than $i_i$ to calculate a different effective section modulus for sustained and occasional stresses (nb. the Code is clear on the fact that corroded thickness is to be used for sustained stress calculations, resulting in two different values where applicable).

This topic is hardly unknown, even being discussed in the excellent “Pipe Stress Engineering” by LC & TL Peng (Section 4.5.1). Their recommended treatment for the sustained effective section modulus is based on the ASME B31.1 approach. The use of $0.75i$ is prescribed for this application in ASME B31.1 (sect 104.8.4C), which makes me wonder why the two committees don’t work together more closely. I have had some correspondence with the B31.3 committee on the matter and am informed that they’re looking into it.

Use of Stress Index from FEA or Testing

If stress index values are calculated by other means such as B31.J, with an index less than $0.75i_i$ , this non-conservatism could be greater, again however it depends on how it is applied and to what section modulus in the software.

Practical implications
Analysts often don’t bother to split a branch element at the wall to check the stress there, because they believe rightly or wrongly that the stress at the intersection is always higher. Users should check whether their pipe stress software is prone to this calculation anomaly under B31.3, and if so, they must remember to split the branch pipe and check the stress at the location immediately before the shell intersection, as the Code sustained stress there may well be higher than at the centreline intersection. Alternatively the software may be configured to use the full SIF for sustained stress calculations.

Code Editions

The use of the sustained stress index came about in the 2010 edition of the ASME B31.3. However the option to use $0.75i$ has existed for many years in some software, leading to similar outcomes. Happily to say that this has not resulted in any failures to our knowledge, thanks to Code safety factors and good design practices such as supporting next to heavy in-line items.

Other Codes – B31.1/4/8 and EN13480

As referred to previously, ASME B31.1 does not suffer from this ambiguity and correctly specifies two different effective modulus formulae for sustained and displacement stresses.

Codes B31.4 & B31.8 are also immune to this issue as they do not use an effective section modulus for reducing branches.

EN13480 does use an effective modulus and at first appearance could be susceptible to this issue, however I have not done any further investigation into this Code as yet.

Martin Blackman

Martin helps clients keep on top of their pressure piping and equipment integrity issues via stress analysis, FEA and fitness for service. He is the author of various articles, an ASME paper and software including the Salad post-processor for CAESAR II and web apps on this site. In a former life he played whizzbang lead guitar, but now he just plays old albums..

B31.3 Code Issue – Non-conservative Sustained Stress